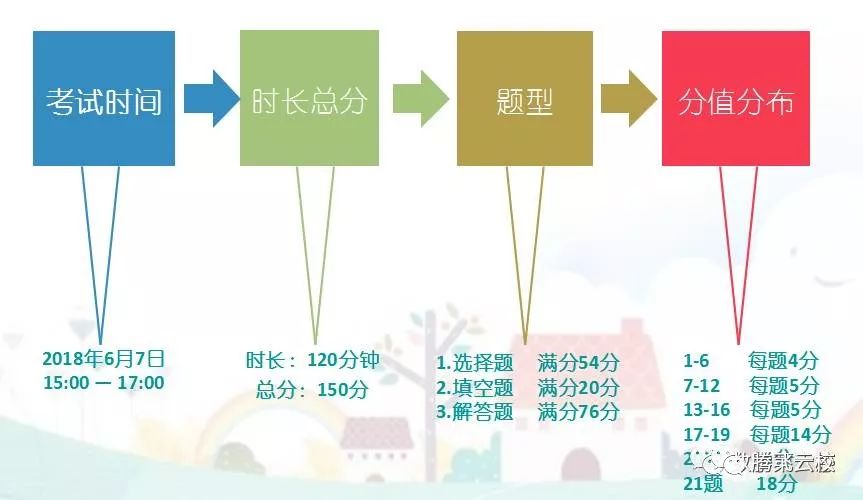
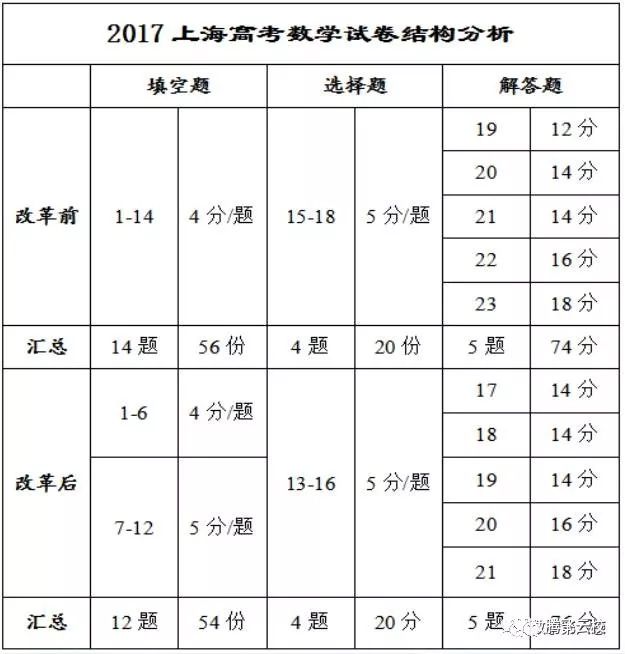
1、2017年上海高考改革，总分保持150分，总题量减少至21题；

2、填空由14题变成了12题，分值由每题4分变成了前六题每题4分，后六题每题5分，体现难易差别化得分；

3、选择题题量、分数均不变，共4题，每题5分；

4、解答题仍为5题，第一道增加2分，其他不变；

5、如此变化之后，填空题是54分，选择题是20分，解答题是76分。

二、知识模块分析

前言：本文将2013年-2017年上海市高考数学试卷涉及到的知识点分为8大模块，分别为代数、排列组合与概率统计、算法与初步、推理与证明、三角函数、平面解析几何、立体几何、高等数学；先分析8大模块的分值占比、考情变化，再分析各模块内部情况，详细如下。

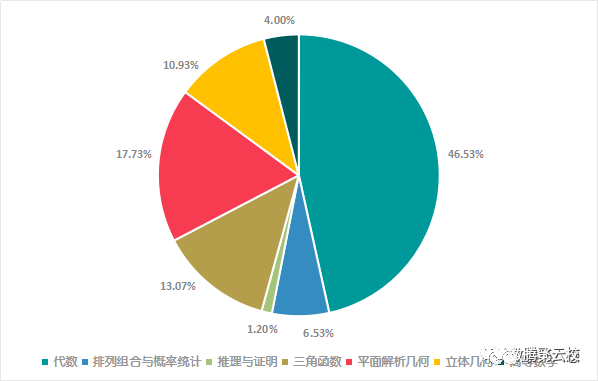
通过上图数据（2013-2017年）可以看出：

1、代数部分在高考占比高达46.53%；

2、平面解析几何占比28.66%，平面解析几何一直为高考难点，考查内容较多；

3、对于推理证明、高等数学方面要求较低，难度低，分值少。

三、近五年命题解读

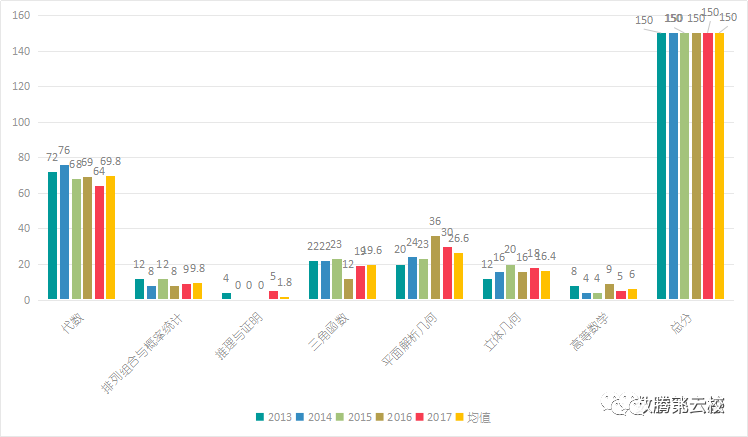
通过上图数据（2013-2017年）可以看出：

1、总分保持在150分；

2、代数分值最高，5年平均值为69.8，占比达到46.53%；

3、推理证明、高等数学等占比最低；

4、每个模块分值波动基本在8分以内。

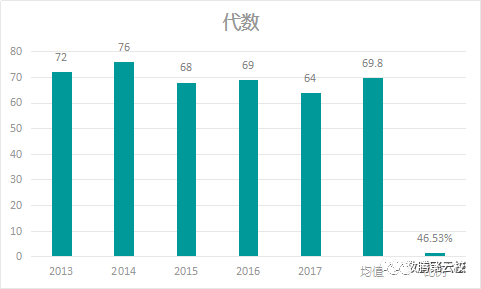
通过上图数据（2013-2017年）可以看出：

1、分数均值为69.8，2017年分值达到近5年最小值，考察要求稍有降低；

2、高考占比高达46.53%，此部分为考试热点；

3、考察内容多，题量大；

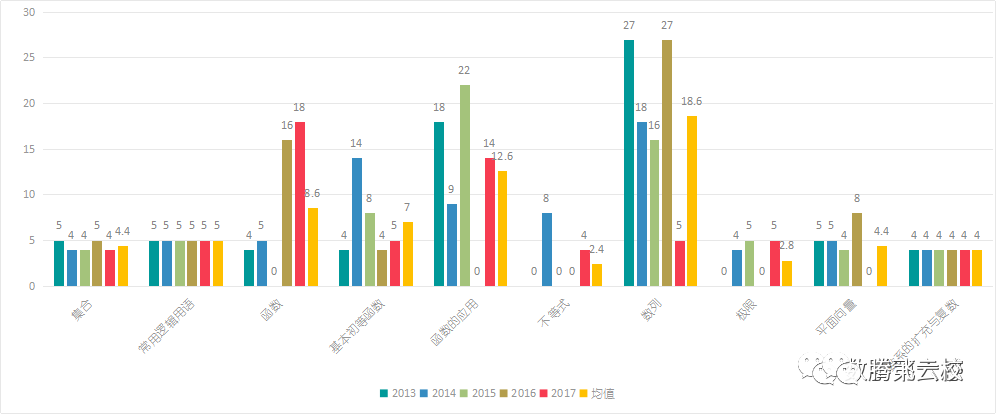
通过上图数据（2013-2017年）可以看出：

1、代数部分考察内容主要在函数、函数的应用、数列三个模块，共占比57.02%，平均每年考察39.8分；

2、不等式近两年开始考察，平面向量17年无考察，这两个模块考察要求变化较大；

3、集合、常用逻辑用语、数系的扩充与复数保持稳定，占比最低；

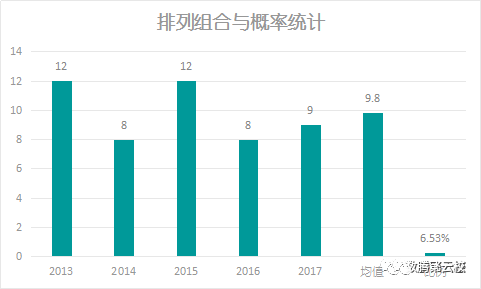
通过上图数据（2013-2017年）可以看出：

1、考察分数均值为9.8，2017年分值较2016年有所上升，但低于平均值，要求稍有降低；

2、高考占比6.53%；

3、考察内容中，题量少；

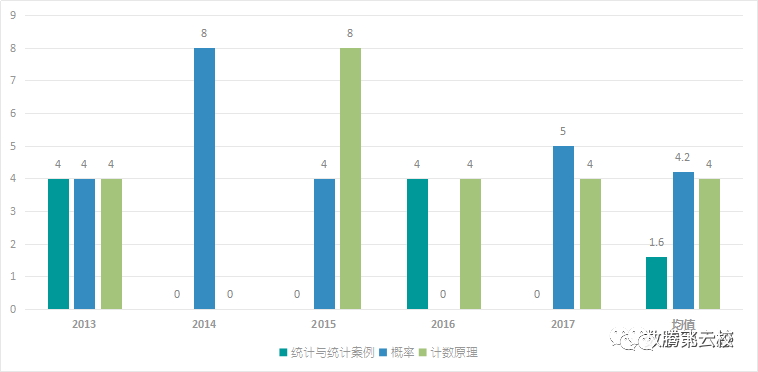
通过上图数据（2013-2017年）可以看出：

1、排列组合与概率统计考察内容主要在概率与计数原理2个模块，共占比83.67%，平均每年考察8.2分；

2、统计与统计案例要求较低，隔年考察；

3、此部分总分稳定在9.8分，内部三模块分值占比变化较大。

通过上图数据（2013-2017年）可以看出：

1、考察分数均值为1.8，2017年分值达到近5年最高值，考察要求稍有提高；

2、高考占比仅有1.20%，此部分为考试冷点；

3、考察内容少，题量少；

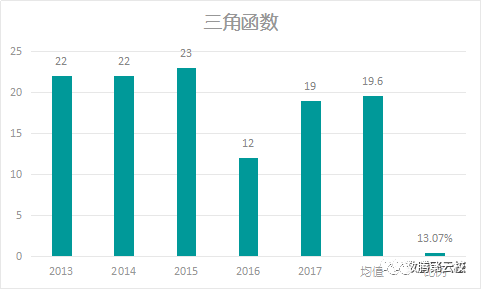
通过上图数据（2013-2017年）可以看出：

1、考察分数均值为19.6，2017年分值较2016年有所上升，但低于近5年均值，要求稍有降低；

2、高考占比13.07%，此部分为考试热点；

3、考察内容多，题量中；

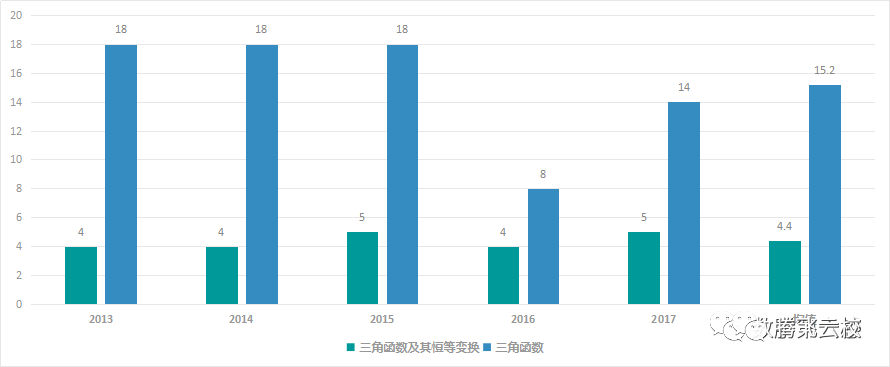
通过上图数据（2013-2017年）可以看出：

1、三角函数部分考察内容主要在三角函数，占比77.55%，平均年考察15.2分；

2、三角函数及其恒等变换与三角函数比例近5年变化不大。

通过上图数据（2013-2017年）可以看出：

1、分数均值为26.6，2017年分值较2016年有所下降，但高于近5年均值，考试要求有所提高；

2、高考占比高达17.73%，此部分为考试热点；

3、考察内容多，题量大；

通过上图数据（2013-2017年）可以看出：

1、平面解析几何部分考察内容主要在圆锥曲线与方程，平均年考察20分；

2、直线与方程考核要求呈现下降趋势；

3、在平面解析几何部分，圆与方程考核要求最低。

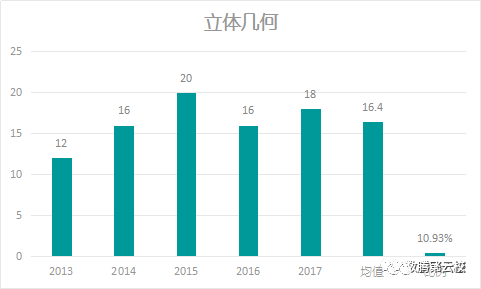
通过上图数据（2013-2017年）可以看出：

1、考察分数均值为16.4，2017年分值较2016年有所上升，且高于近5年均值，考察要求稍有提高；

2、高考占比10.93%，此部分为考试热点；

3、考察内容多，题量大；

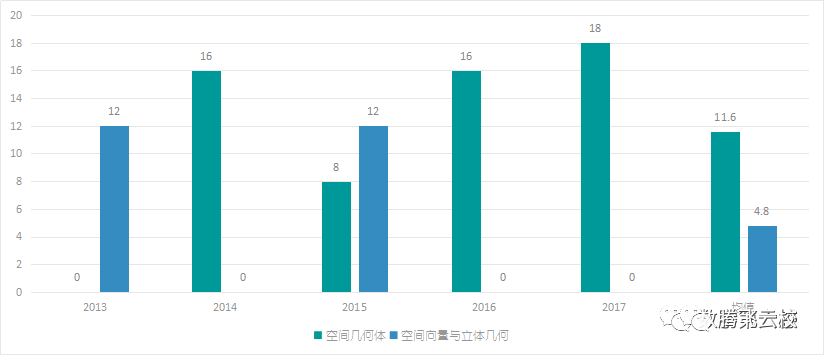
通过上图数据（2013-2017年）可以看出：

1、立体几何部分考察内容主要在空间几何体，占比70.73%，平均年考察11.6分；

2、2014、2016、2017三年，没有考察空间向量与立体几何；

3、近5年分值在16.4分附近波动。

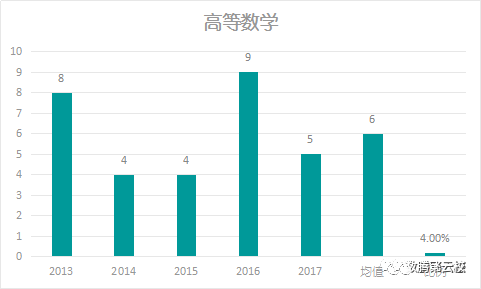
通过上图数据（2013-2017年）可以看出：

1、考察分数均值为6，2017年分值较2016年有所下降，且低于近5年均值，考察要求稍有降低；

2、高考占比4.00%，此部分非热点部分；

3、考察内容少，题量少；

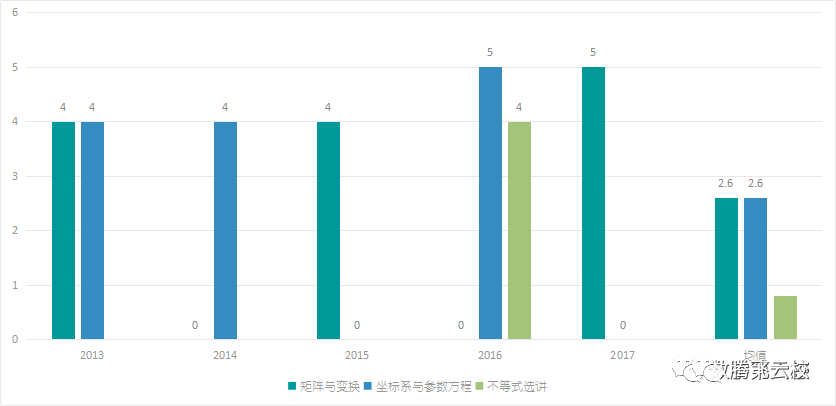
通过上图数据（2013-2017年）可以看出：

1、高等数学部分考察内容主要在矩阵与变换、坐标系与参数方程2个模块，共占比86.67%，平均年考察5.2分；

2、不等式选讲只有2016年考察4分，要求相对较低；

3、矩阵与变换、坐标系与参数方程考核要求相近，近5年均值相等。

四、复习备考

一、重视双基，回归课本

同学们在复习的时候，一定要关注定理、结论、公式的推导方法及过程，注意这些方法在其他方面的应用，重视知识方法的迁移。

二、提高解决实际应用问题的能力